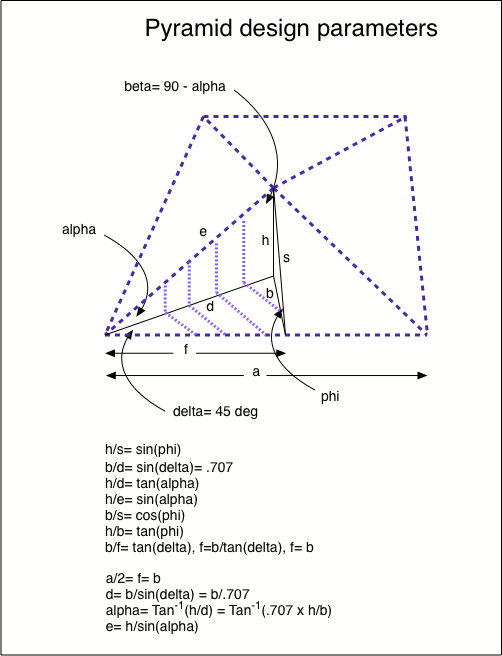
The following formulae make it easy to figure out the length of the pyramid's sides, for example, after applying other constraints such as the angle of the sides and the height. This is useful if one wants to build a pyramid for experimentation.
 |
| Figure 1. Formulae for designing a pyramid shape. |
Example: We want a pyramid where the ratio (the distance from the bottom to the top) / (half the base) (i.e., s/b) is the golden ratio (1.618).
s/b= 1.618
so cos(phi)= b/s= 0.618
then phi= 51.827 deg
if a= 6, then b= 3 and h= a/2 x tan(phi)= 3.816
alpha= Tan-1(.707 x h/b)= 41.965 deg
e= h/sin(alpha)= 3.816 / 0.6686= 5.71
So if the base of the pyramid is 6 in, then the edge of a side must be 5.71 in.
The angle of 51.827 degrees is also the angle of the side of the Great Pyramid of Giza (Cheops).