
Summary. A crop formation that appeared near Wilton Windmill, Wiltshire, on May 22, 2010, contains a set of bits that appears to simultaneously represent two meaningful text strings and four images showing familiar objects. One text string is an approximation to Euler's identity, and the other represents an algorithm for decoding an ASCII symbol sequence to an image format. The algorithm was initially applied to the ASCII data from the 2002 Crabwood formation. The resulting image was interpreted as a representation of a bipedal figure extending a three-fingered hand in greeting. In this article, the same algorithm was applied to 288 bits of data from the Wilton Windmill formation. Remarkably, four meaningful images were generated from the same data set by using different spatial bit sampling schemes. One image appears to show a face with large ears as in a drawing of a bunny in a child's book. Another shows what appears to be a child riding a tricycle. The final two images show a humanoid body in different poses with one arm raised. The presumed "hi" error that appeared in the decoded Euler's identity clearly shows that the raised arms are intended as a greeting. The common feeling from these images is that they are non-threatening. Perhaps the message they are intended to convey is that we should not fear possible encounters with the makers of these formations.
A crop formation appeared near Wilton Windmill, Wiltshire, on May 22, 2010. The design suggested to a number of people that the formation contains sequences of ASCII characters.
 |
Figure 1. The Wilton Windmill formation. |
The formation quickly became famous when someone decoded Euler's identity, a well-known mathematical formula, from the ASCII symbols impressed on the flattened vegetation. The formula began in the sector just to the right of the tram line at the 10-o'clock position in Figure 1. Each arc protruding from a radial line was read as a 1 and the absence of an arc was read as a 0. On one side of each radial line, the bit nearest the center was always 0, and only this side was used. Since the bit nearest the center was constant, it was ignored. The remaining seven bit positions were used to create a 7-bit ASCII character code, starting from the second bit position and moving towards the circumference. Successive characters were read from adjacent radial lines moving in the clockwise direction. A file containing the twelve character codes may be seen here. The text string "e^(hi)pi)1=0" decoded from this data was recognized as a close approximation to "e ^ (i pi) + 1 = 0", the correct form of the equation. Some have noted that the extraneous 'h' symbol forming the word "hi" may have been intended as a greeting.
Subsequently, another text string was found by an anonymous participant in a discussion group on the Crop Circle Connector website (this page now accessible by subscribers only). Each character in this string was decoded from the other side of each radial line, with bits read from the circumference towards the center. Again, the bit nearest the center was ignored since it was constant. A file containing these twelve 7-bit character codes may be seen here. The text string ",But45x459!y" decoded from this data was not meaningful to the anonymous discoverer, but it is recognized here as a high-level algorithm for transforming ASCII symbols into a visual format.
The string contains two numbers, 45x459, that are both divisible by nine. They may be rewritten as 9x9x255. The number 255 is the maximum decimal value of an 8-bit (or byte) character code that represents the intensity of a pixel in a grayscale image. The 9x9 could specify the size in pixels of an image array. Finally, the "!y" characters could mean that the bits in each y byte are to be negated. The ! symbol is the logical NOT operator in some computer programming languages. Therefore, a translation of the original text string could be ", but see the image decoded using 9x9 arrays of bytes with bits inverted". Computer code implementing this algorithm can be seen here.
This image decoding algorithm was first applied to an existing ASCII data set derived from the 2002 Crabwood formation. A previous article gives more information about the formation and the data. Figure 2 shows the image decoded from that data set. It might be interpreted as a representation of a bipedal figure extending a three-fingered hand in greeting.
 |
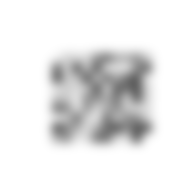 |
| Original image | Gaussian blur |
| Figure 2. Image decoded from the Crabwood formation. | |
The search continued for other ways to to interpret the Wilton Windmill formation. Could it also contain sufficient information to encode an image? An interesting approach was suggested in an article by Zef Damen. His reconstruction of the formation offered a way to decode 36 bytes of data which would be enough to represent a 9x4 image array. The approach takes advantage of the observation that the arcs projecting from the 12 radii are not all the same length, so that between each pair of dashed lines left in from the reconstruction process there may be a different number of bits of the arcs. Each bit encountered represents a 1 for that bit position, else that position is a 0. This basis for bit assignment is shown in the diagram of Figure 3.
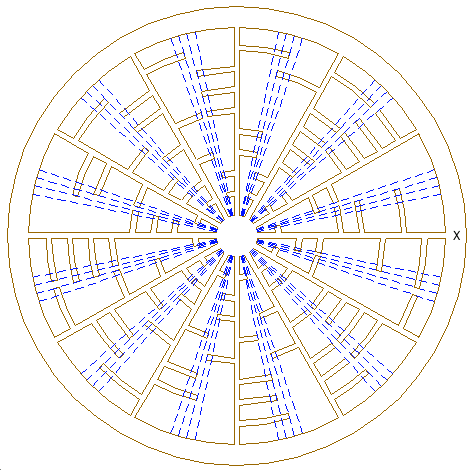 |
Figure 3. Zef Damen's reconstruction of the Wilton Windmill formation. |
A total of 288 bits were obtained using this approach. This gives 36 bytes of data, sufficient for a 9x4 image array. Four different and apparently meaningful images were found in the same set of bits read from the formation in different ways. The starting point was always the inner ring of the radial line, marked by an X in Figure 3, that gave the first symbol of Euler's formula. The meaningfulness of the images is subjective, of course, and the reader may agree or disagree with the interpretations given.
For the first image found in the formation, each byte was built up of bits assigned going from the center to the outer rim for every pair of adjacent dotted lines progressing clockwise. The data file may be seen here. The algorithm then inverted the bits and assigned the resulting byte value to a pixel of the 9x4 grayscale image. The result was the image shown on the left in Figure 4. The image smoothed with a Gaussian blur filter is shown on the right. Perhaps it can be interpreted as a face with large ears as in a drawing of a bunny in a child's book.
 |
 |
| Original image | Gaussian blur |
| Figure 4. First image decoded from the Wilton Windmill formation. | |
For the second image, the order of the bits was altered according to a hint from Euler's formula, which can be expressed in terms of the trigonometric sine and cosine. The bits in the first byte were read from the center to the outside. Moving clockwise to the adjacent pair of dotted lines, the second byte was read from the outside to the center, the third was read from the center to the outside, etc. This sinusoidal pattern continued until all 36 bytes were constructed. The data file may be seen here. Again, the display algorithm inverted the bits and assigned the byte values to the 9x4 array of image pixels. The result was a picture shown in the first row of Figure 5. The smoothed image is easily interpreted as the frontal view of a humanoid figure with head tilted to the side and left arm waving.
If we think of the order of the bits in the previous image as being read in sine phase, we can construct a third image by reading the bits in cosine phase. To do this, the bits in the first byte were read from the outside to the center, the second was read from center to the outside, the third was read from outside to the center, etc. This pattern continued until all 36 bytes were constructed. The data file is here. After inverting the bits, the bytes were assigned to the 9x4 pixel array. The result is shown in the second row of Figure 5. Remarkably, the smoothed version is a similar humanoid figure, this time appearing to be stepping away while waving with the right arm.
| Sine phase |  |
 |
|---|---|---|
| Cosine phase | 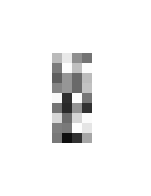 |
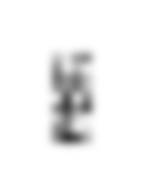 |
| Original image | Gaussian blur | |
| Figure 5. Second and third images decoded from the Wilton Windmill formation. | ||
The sine phase image seems approximately mirrored by the cosine phase image. Might this visual effect be a trivial result of the mirrored patterns of reading the bits? This possibility was tested empirically by generating random data as sine phase data, then reordering that data manually to simulate the cosine phase data. The result of this test clearly shows that the procedure itself is not sufficient to account for the approximate mirror image. Apparently, the similarity of the two images was intended by the designer of the formation.
The fourth image generated from the formation organized the bits according to their positions in the eight concentric circles. That is, the bits were read by going around each consecutive circle in the clockwise direction, beginning at the inner circle. The data file may be seen here. As before, the algorithm inverted the bits and assigned the resulting byte value to a pixel of the 9x4 grayscale image. The result was the image shown on the left in Figure 6, with the smoothed version shown on the right. The object in the image could easily be a child riding a tricycle.
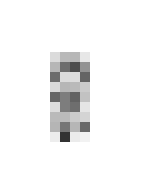 |
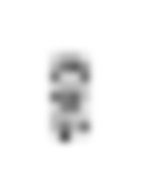 |
| Original image | Gaussian blur |
| Figure 6. Fourth image decoded from the Wilton Windmill formation. | |
In retrospect, the two images in Figure 5 appear to be related to the way the data bits were organized. The images were obtained by up-and-down ordering of the bit arrays forming each byte as suggested by the trigonometric form of Euler's formula. This sinusoidal motion is what one would expect from the waving arm in each image. It also seems appropriate that the mirrored sinusoidal sampling patterns resulted in images in which opposite arms are raised. Further, the reason for the apparent error in the decoded Euler's identity now seems obvious. The "hi" substring is intended to show us that the raised arms in the images are to be interpreted as a greeting.
The other images can also be related to the particular bit orders used in their construction. The image of Figure 6 was obtained by going round-and-round the circles to extract the bytes. Of course, prominent features of a tricycle are its circular, different-sized wheels. The relation for Figure 4 is perhaps not as obvious. Maybe the alert, raised ears of the rabbit can be related to the diverging construction lines in Figure 3 guiding the strictly inner-to-outer ordering of the bits.
Some may think that the interpretations of the images are too subjective, and that each image may just be an array of random pixel values. To address this issue, the same arrays were also processed with offsets of 1-7 bits, and the resulting smoothed images are presented here. The objects in the images with no offset appear to be more recognizable than in the images with offsets. This would be expected if the images with zero offset were intended by the designers of the formation.
It is amazing that someone was able to arrange a set of bits in this formation in such a way that two interpretable text strings and four meaningful images could be decoded simply by choosing different byte selection schemes. Not only was the same set of bits used, but the bit values were constrained to be complementary on each side of a given radial line in the formation. That is, if a 1 was represented on one side of a line, then the other side always represented a 0, or vice versa. Successfully encoding this much meaningful text and image information in such a co-dependent way is very unlikely to have happened by chance. It might have been done by optimizing an appropriate cost function, if one could even be defined. That the encoding was intentional is strongly supported by the conceptual similarity of the two images of Figure 5 decoded using hints from Euler's formula. Each image shows a humanoid figure with an arm raised perhaps in greeting. The obvious similarity is persuasive confirmation that the data sampling schemes were correct and the decoding algorithm was applied as intended.
The decoded images all appear to contain rather trivial content. What we can say, however, is that an image of a proffered handshake, the face of a fuzzy animal, a friendly wave, and a child riding a tricycle, have one thing in common. Such images are particularly non-threatening. Perhaps this is the message. If the crop formations are a prelude to an actual meeting with the designers of the formations, these images may be telling us to have no fear when this event occurs.